The Schrödinger Equation: Waves of Probability

Introduction: Setting the Stage for the Quantum Dance

In the vast tapestry of the universe, there exists a realm so peculiar and fascinating that it challenges the very fabric of our everyday understanding. Welcome to the Quantum Realm, a domain where particles dance in waves of probability, and where the classical laws of physics we’re so familiar with seem to be suspended.

At the heart of this realm lies the Schrödinger Equation, a fundamental piece in the quantum jigsaw. It’s more than just a mathematical expression; it’s the key that unlocks the door to the bizarre behaviors exhibited by particles at the quantum level. This equation, introduced by Erwin Schrödinger in the 1920s, has become a cornerstone of quantum mechanics, guiding scientists in their quest to understand the underlying nature of the universe.

As we embark on this journey, we’ll be navigating the waves of probability, diving deep into the essence of the Schrödinger Equation, and exploring its many facets and implications. From understanding the core tenets of wave functions and probability densities to drawing parallels with our everyday experiences, this exploration promises to be both enlightening and perplexing.

Why does this equation matter? How does it challenge our classical understanding of the world? And, most importantly, what can we learn from it about the nature of reality itself? These are just some of the questions we’ll be delving into. So, buckle up and prepare for a ride into the mysterious depths of the quantum world.

Foundations of Quantum Mechanics: Delving into the Quantum Bedrock

Quantum mechanics can be likened to a vast, mysterious ocean, teeming with wonders that defy our classical intuitions. Before we plunge deeper into the specific waves of the Schrödinger Equation, it’s crucial to get acquainted with the basic currents that flow in this ocean.

A Brief Recap of Quantum Mechanics Basics:

Quantum States: At the quantum level, particles exist in states that describe all their possible properties. Unlike classical physics, where a particle has a definitive position or momentum, quantum mechanics embraces a realm of probabilities.
Superposition: A cornerstone of quantum mechanics, superposition posits that particles can exist in multiple states simultaneously. It’s only upon observation that they ‘collapse’ into a single state.
Entanglement: One of the spookiest phenomena, entanglement describes a connection between particles such that the state of one particle immediately affects the state of another, regardless of the distance between them.
Quantization: At the quantum level, properties like energy don’t vary continuously but come in discrete, ‘quantized’ packets. This was groundbreaking when first proposed, as it deviated from the continuous nature of classical physics.

Key Concepts and Terminologies:

Wave Function (Ψ): This mathematical function provides a complete description of a quantum system. It’s the heart of the Schrödinger Equation and encodes all possible information about a particle.
Operators: In quantum mechanics, physical quantities like momentum or energy are represented by mathematical operators that act on the wave function.
Eigenstates and Eigenvalues: When an operator acts on a specific wave function (an eigenstate), it yields a scalar multiple of that wave function (the eigenvalue). This concept is pivotal in understanding quantum measurements.
The Principle of Superposition: As mentioned, particles can exist in a combination of states. When measured, the wave function collapses, and the system assumes one of these states.
Quantum Tunneling: A phenomenon where particles move through barriers they classically shouldn’t be able to, hinting at the probabilistic nature of quantum mechanics.

As we navigate through the complexities of the Schrödinger Equation and its profound implications, these foundational concepts will be our guiding stars. They not only form the bedrock of our understanding but also open doors to the myriad mysteries the quantum realm holds.

Introducing the Schrödinger Equation: A Harmonic Dance of Quantum Waves

Quantum mechanics is replete with equations that challenge our understanding of reality, but few are as central or as enigmatic as the Schrödinger Equation. This equation is the linchpin that holds together our understanding of quantum dynamics.

The Birth of the Schrödinger Equation: Historical Context

The 1920s marked a revolutionary period in physics. The established norms of classical physics were under scrutiny, and a new framework was desperately needed to explain perplexing phenomena at atomic and subatomic levels.
Amidst this backdrop, in 1926, the Schrödinger Equation was born, offering a wave description of particles that contrasted with the particle-like behavior described by Heisenberg’s matrix mechanics.
This equation provided a new lens to view and understand the behavior of quantum systems, setting the stage for much of modern quantum mechanics.

Erwin Schrödinger: The Man Behind the Equation

Erwin Schrödinger, an Austrian physicist, was not just a mathematician but also a philosopher at heart. His inquisitiveness led him to ponder the fundamental nature of particles and waves.
Inspired by Louis de Broglie’s proposition of wave-particle duality, Schrödinger sought a unifying equation that could seamlessly describe this duality. His efforts culminated in the Schrödinger Equation.
Beyond his equation, Schrödinger is also renowned for his thought experiments, most notably “Schrödinger’s cat”, which highlights the paradoxes of quantum superposition.

The Equation Unveiled: A Look at its Mathematical Form and Essence

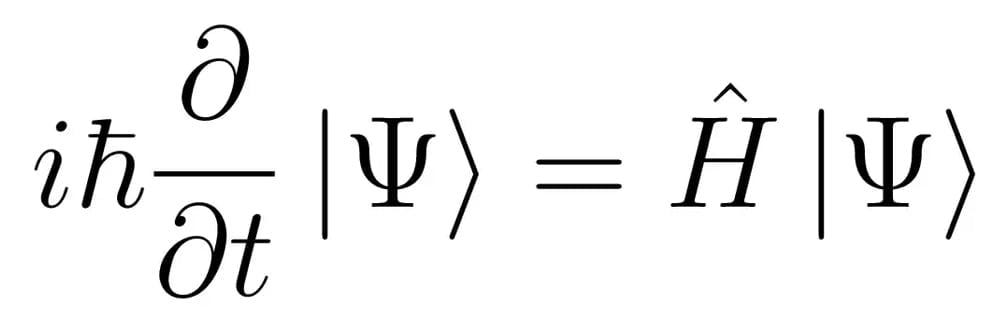
At its core, the Schrödinger Equation describes how the quantum state of a physical system changes over time.
Here, Ψ is the wave function of the system, ℏ is the reduced Planck’s constant, and H^ is the Hamiltonian operator, representing the total energy of the system.
The equation beautifully marries the concepts of energy conservation with wave propagation, providing a complete description of a quantum system’s evolution.

The Schrödinger Equation is not merely a mathematical construct; it’s a doorway to understanding the very heart of the quantum realm. As we delve deeper into this topic, this equation will serve as our guiding light, illuminating the intricate dance of particles in the quantum world.

Probability Density and Wave Functions: Surfing the Quantum Seas

At the heart of quantum mechanics, beyond equations and rigorous mathematics, lies a world teeming with waves. These aren’t the waves you’d find crashing against the shore; these are quantum waves, and understanding them is pivotal to grasping the Schrödinger Equation and the mysterious realm it describes.

Riding the Quantum Waves: Understanding Wave Functions

The wave function, often denoted as Ψ, is a mathematical expression that encapsulates all the information about a quantum system. It describes the state of a particle in terms of position, momentum, spin, and more.
Unlike classical physics where properties are definitive, in quantum mechanics, these are probabilistic. The wave function gives a probabilistic account of where a particle might be found or how it might behave.
It’s important to note that the wave function itself isn’t directly observable. Instead, it serves as a tool to predict probabilities.

The Essence of Probability Density: What It Represents and Its Significance

When we square the magnitude of the wave function, ∣Ψ∣^2, we obtain the probability density. This tells us the likelihood of finding a particle in a particular position at a given time.
Think of probability density as a topographical map, where peaks indicate higher probabilities and troughs represent lower ones. Just as you’d expect more rainfall at the peak of a mountain than in a valley, you’d expect to find the particle more often where the probability density peaks.
This concept diverges from classical intuition. Instead of having a definite position, quantum particles have areas where they are more or less likely to be found.

Visualizing Probability Densities: Peaks, Troughs, and Everything in Between

Visual representations are crucial in quantum mechanics, especially when grappling with abstract concepts. For wave functions and probability densities, graphical plots provide invaluable insights.
When plotting ∣Ψ∣^2 against position, we might see a single peak, indicating a particle is likely localized in that area. Or, we might see multiple peaks, suggesting the particle could be in multiple places with varying probabilities.
These plots not only offer a snapshot of the quantum state but also guide physicists in predictions and experiments, allowing them to test the boundaries and veracity of quantum theory.

In the grand tapestry of quantum mechanics, wave functions and probability densities are threads that weave together to form the intricate patterns we seek to understand. As we delve deeper, keep these concepts in mind, for they’ll be our constant companions on this quantum odyssey.

The Time-Dependent and Time-Independent Forms: Quantum Choreography Through Time

Time is an ever-present dimension in our understanding of the universe. It governs our daily lives, the orbits of planets, and even the flow of light across space. But in the quantum realm, time takes on a dance of its own, with the Schrödinger Equation as its choreographer.

The Dance of Time: Distinguishing Between the Two Forms

Much like a piece of music having various tempos or styles, the Schrödinger Equation exists in two primary forms that describe quantum systems in different time contexts.
These two forms are not merely mathematical variations but encapsulate different physical scenarios and predictions.

The Time-Dependent Schrödinger Equation (TDSE): Delving into Dynamic Quantum States

The TDSE, with time as an explicit factor, captures the evolution of quantum systems. It’s the equation of motion for quantum mechanics, detailing how quantum states change with time.
Imagine watching a dancer on stage, every twirl, leap, and step dictated by the rhythm of the music. Similarly, TDSE describes the dynamic ‘dance’ of particles as they evolve.
It’s essential for scenarios where quantum states are not static, such as during a measurement or when a particle is in a superposition of states.

The Time-Independent Schrödinger Equation (TISE): Exploring Stationary States and Implications

The TISE, on the other hand, focuses on stationary states. These are quantum states that don’t change their form over time, though they might still oscillate or ‘vibrate’.
Think of it as a snapshot of a dancer in mid-air, frozen in time, capturing the essence of motion without the temporal progression.
While the particle’s properties (like energy) are definite in these states, its position is still described probabilistically. TISE gives us the possible energy levels a quantum system can have, shedding light on atomic orbitals, energy bands in solids, and more.

Understanding the two forms of the Schrödinger Equation is like appreciating both the still photographs and the video footage of a dance performance. One captures the essence, while the other portrays the progression. Together, they offer a comprehensive view of the mesmerizing choreography of particles in the quantum world.

The Real-life Analogies: Bridging Quantum Concepts with Everyday Experiences

Quantum mechanics often feels like a realm completely detached from our everyday experiences. But, just as poets use metaphors to illustrate abstract feelings, we can use real-life analogies to illuminate the elusive concepts of the Schrödinger Equation.

Waves on a Pond: Understanding Wave Functions

Imagine tossing a pebble into a calm pond. The ripples that emanate from the point of impact are similar to the quantum wave function. Just as each ripple carries energy and information about the initial disturbance, the wave function encodes information about a particle’s state.
But, unlike our pond, where we can predict the exact trajectory of a ripple, in the quantum world, the wave function only gives us probabilities. It’s as if each ripple in our pond has a mind of its own, choosing its path based on chance.

A Crowd in a Stadium: Grasping Probability Density

Consider a packed stadium during a concert. From a bird’s eye view, some sections of the crowd might be densely packed, while others are sparse. This distribution can be likened to the probability density associated with a particle’s position.
Just as certain sections of the stadium are more likely to have a person (high crowd density), certain regions in space have a higher probability of finding our quantum particle (high probability density).

Mountain Peaks and Valleys: Visualizing Probability Densities

Imagine a mountainous landscape, with towering peaks and deep valleys. If this landscape represented our probability density, the peaks would signify where we’re most likely to find a particle, while the valleys are where it’s least likely to be.
But unlike static mountains, these quantum ‘landscapes’ can change over time, morphing based on external influences and the particle’s inherent properties.

These analogies, while not perfect, offer a bridge between the abstract world of quantum mechanics and the tangible reality we experience daily. They provide a lens to view and appreciate the complexities of the Schrödinger Equation, making the esoteric slightly more familiar.

The Equation in Action: Case Studies

The Schrödinger Equation, while steeped in abstract concepts and intricate mathematics, is far from being a mere theoretical exercise. Throughout the decades, it has been employed in a multitude of real-world scenarios, showcasing its undeniable utility and transformative power. Let’s delve into a few case studies that highlight its practical applications.

Molecular Bonding and Chemistry

At the core of every chemical reaction lie the interactions and bonds between atoms and molecules. The Schrödinger Equation plays a pivotal role in predicting molecular structures and understanding chemical reactivity. For instance, chemists use the equation to determine the likelihood of an electron being in a certain region around two bonded atoms, providing insights into bond strengths and lengths.

Semiconductor Physics and Modern Electronics

The electronics that power our modern world, from smartphones to computers, rely on semiconductors. The behavior of electrons in these materials, especially in quantum wells and quantum dots, is governed by the Schrödinger Equation. By solving this equation for specific scenarios, engineers can design novel electronic devices with enhanced properties.

Drug Design and Pharmaceutical Research

The world of drug discovery often requires a deep understanding of how potential drug molecules will interact with biological structures. By applying the Schrödinger Equation to these molecules, researchers can predict their behavior, interaction sites, and potential efficacy, paving the way for more targeted and effective drug therapies.

Quantum Wells and Lasers

Quantum wells, thin layers that confine particles in one dimension, have been instrumental in the development of advanced lasers and optoelectronic devices. The Schrödinger Equation is used to determine the electron energies in these wells, influencing the design and efficiency of the resulting devices.

Understanding Superconductivity

Superconductors, materials that conduct electricity without resistance, have mystified and intrigued scientists for over a century. By applying the Schrödinger Equation to these materials, researchers gain insights into the behavior of electron pairs, helping to explain and potentially harness this phenomenon for future technologies.

These case studies offer just a glimpse into the myriad applications of the Schrödinger Equation. Its influence spans numerous fields and industries, making it one of the cornerstones of modern science and technology.

Comparative Insight: Classical vs. Quantum Physics

In the grand tapestry of physics, two major threads emerge: the well-established classical physics and the enigmatic quantum physics. As we delve deeper into the Schrödinger Equation, it’s vital to discern its position in this dichotomy, and understand how it offers a departure from classical predictions.

Classical Physics: The Familiar World Classical physics, encompassing the laws of mechanics laid out by Sir Isaac Newton, is a realm of predictability. It deals with macroscopic objects, where the position and momentum of a particle can be precisely determined. In this deterministic universe, if we knew all the conditions of a system at a particular time, we could predict its future state with absolute certainty.

Quantum Physics: The Realm of Probabilities Enter the quantum realm, and this predictability crumbles. At the atomic and subatomic scales, particles behave in ways that defy classical intuition. Instead of deterministic outcomes, we’re introduced to a world governed by probabilities. The Schrödinger Equation is at the heart of this, providing a mathematical framework to describe these probabilistic behaviors.

How the Schrödinger Equation Deviates While classical physics might predict a particle to be in a specific place at a specific time, the Schrödinger Equation offers a wave function that describes the probability of finding a particle in a particular location. There’s no certainty, only likelihood. This is a profound shift, where particles don’t have definite positions or speeds until they are observed.

The Double Slit Experiment: A Stark Illustration Consider the famous double-slit experiment. Classical intuition suggests that particles, like electrons, should pass through one slit or the other. However, when not observed, these particles exhibit wave-like interference patterns, as if they passed through both slits simultaneously. The Schrödinger Equation can describe and predict this baffling behavior, showcasing its deviation from classical predictions.

The Revolutionary Nature of Quantum Mechanics Quantum mechanics, with the Schrödinger Equation as one of its foundational pillars, has revolutionized our understanding of the universe. It challenges our very notions of reality, pushing us to accept a non-deterministic, probabilistic world at its fundamental level. Yet, it’s this very framework that has enabled advancements in technology, from semiconductors to lasers, solidifying its crucial role in modern science.

In this intricate dance between the classical and quantum, the Schrödinger Equation stands as a testament to the mysteries and wonders of the universe, offering insights that continue to shape the very fabric of physics.

The Challenges and Controversies

The unveiling of the Schrödinger Equation in the quantum realm was by no means a smooth affair. Like many scientific innovations that drastically shift paradigms, it too faced its share of skepticism, challenges, and controversies.

Schrödinger’s Initial Skepticism and Challenges When Erwin Schrödinger first formulated his equation, even he was taken aback by the implications. He found himself at odds with the probabilistic interpretation, feeling uneasy about a description of reality based on probabilities rather than certainties. Moreover, the revolutionary nature of his equation, which posited wave-like behaviors for particles, was so radical that it was bound to stir skepticism and resistance, not just from the broader scientific community, but also from within Schrödinger himself.

Debates in the Scientific Community The introduction of the Schrödinger Equation ignited fervent debates among physicists. One of the most famous disputes was between Schrödinger and Werner Heisenberg, another quantum pioneer. While both their formulations (wave mechanics by Schrödinger and matrix mechanics by Heisenberg) were eventually found to be equivalent, the two had starkly different views on the best way to describe quantum phenomena.

Moreover, the philosophical implications of the equation, particularly its probabilistic nature, were deeply unsettling to many, including Albert Einstein. Einstein’s famous remark, “God does not play dice with the universe,” epitomized the discomfort many felt with this new quantum description of reality.

Issues of Interpretation Beyond the mathematical form of the equation, the larger question of its interpretation loomed large. What does it mean to describe particles as waves of probability? Does a particle truly exist in a superposition of states until observed? These questions gave rise to numerous interpretations of quantum mechanics, from the Copenhagen interpretation, which posits that the act of observation collapses the wave function, to the many-worlds interpretation, which suggests every quantum event leads to a branching of the universe.

A Legacy of Unsettled Questions While the Schrödinger Equation has withstood the test of time and experiment, the philosophical and interpretative questions it raises remain subjects of debate to this day. As we venture deeper into the quantum world, we find that the challenges and controversies surrounding this equation are not mere historical footnotes but are integral to our ongoing quest to understand the nature of reality.

The Schrödinger Equation and Popular Culture

The realm of quantum mechanics, with its bewildering concepts and paradoxes, has not only captivated the minds of scientists but has also found its way into the tapestry of popular culture. The Schrödinger Equation, emblematic of this quantum world, has been referenced, alluded to, and celebrated in various forms of art, cinema, literature, and even casual conversations.

Movies and the Quantum Dance The world of cinema, with its penchant for the dramatic and the mysterious, has occasionally dipped its toes into the quantum pool. Films like “What the Bleep Do We Know!?” explore the realm of quantum physics and its implications on reality, while the idea of superposition – a core concept associated with the Schrödinger Equation – has been alluded to in movies like “Coherence” and “A Serious Man.”

Literary Allusions Literature, with its vast expanse and depth, has given writers the canvas to explore and play with quantum concepts. Novels such as “The Quantum Thief” by Hannu Rajaniemi and “Anathem” by Neal Stephenson weave quantum mechanics into their narratives. But perhaps the most famous literary nod to the Schrödinger Equation is the thought experiment known as “Schrödinger’s Cat,” which has been referenced in countless books, essays, and discussions.

Artistic Representations The world of art, ever-abstract and interpretative, has seen artists drawing inspiration from the Schrödinger Equation. From visual art pieces depicting wave functions and probability clouds to musical compositions resonating with the harmonics of quantum states, the influence is palpable.

Everyday Conversations and Jokes The phrase “Schrödinger’s Cat” has become a part of everyday lexicon, often used humorously to describe situations that have binary outcomes yet to be realized. From memes on the internet to casual banter, the Schrödinger Equation and its associated concepts have become emblematic of the unknown and the mysterious.

Making Quantum Relatable By featuring in popular culture, the Schrödinger Equation and its intricate dance of probabilities have been made more accessible and relatable to the layperson. These references, while often not entirely scientifically accurate, serve to ignite curiosity and wonder, prompting more people to delve deeper into the mesmerizing world of quantum mechanics.

Tying it to the Series

As we journey through the vast and intricate tapestry of quantum mechanics, each chapter of this series has been a stepping stone, unveiling layers of complexity and wonder. From our initial forays into the Quantum Realm to the profound revelations of the Schrödinger Equation, we’ve navigated the waves of probability, surfed the peaks and troughs of wave functions, and marveled at the dance of particles and waves.

Reflecting on Our Quantum Voyage Looking back, our exploration started with the basic tenets of quantum mechanics, setting the foundation upon which our understanding would grow. We delved into the historical contexts, met the trailblazing scientists, and unraveled the mathematical intricacies that govern this microcosm. With each article, we’ve pieced together a segment of the quantum puzzle, and the picture, although never fully complete, has become clearer.

A Glimpse of What’s Next Yet, as with all epic tales, our quantum narrative is far from its climax. While the Schrödinger Equation has been a central character in our story, the next chapter promises even more enthralling mysteries. Prepare to be introduced to one of the most enigmatic and debated phenomena in quantum mechanics: Quantum Entanglement. Often dubbed as ‘spooky action at a distance’ by Einstein himself, this phenomenon challenges our very understanding of reality and locality.

Glossary

Wave Function (Ψ): A mathematical function that describes the probability amplitude of a quantum system. It’s a central concept in quantum mechanics and provides information about the probability distribution of a particle.
Probability Density: It provides the likelihood of finding a particle in a particular position. It’s derived from the wave function and gives a clearer picture of a particle’s location.
TDSE (Time-Dependent Schrödinger Equation): A form of the Schrödinger Equation that considers the changes of a quantum system over time.
TISE (Time-Independent Schrödinger Equation): Describes the quantum state of a system that doesn’t change over time, often used for stationary states.
Quantum Entanglement: A quantum phenomenon where particles become interconnected and the state of one particle immediately affects the state of the other, regardless of the distance between them.