Welcome to another enlightening journey into the world of machine learning at RabbitML. Today, we’re diving deep into the realm of convolutions – a fundamental concept that powers the impressive capabilities of neural networks.
The Magic of Convolutions
Convolutions are the magical spells that transform the raw pixel data of an image into a form that a neural network can understand and process. They are the first step in the journey of an image through a convolutional neural network (CNN), a type of neural network that has proven remarkably effective at image recognition tasks.
Convolutions are a process that transforms the raw pixel data of an image into a form that a neural network can understand and process.
The magic of convolutions lies in their ability to extract features – the important bits of information – from an image. These features could be anything from the edges of an object to more complex patterns like shapes or textures. The more complex the feature, the deeper into the network it is typically found.
The Convolution Operation
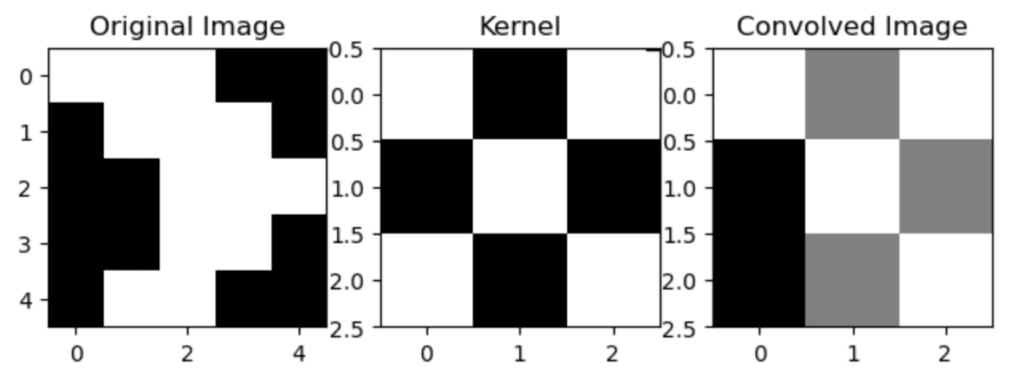
The convolution operation itself is a relatively simple mathematical operation. It involves sliding a small matrix, known as a kernel or filter, over the input image. At each step, the kernel is multiplied element-wise with the part of the image it is currently on, and the results are summed up to give a single output pixel in the feature map.
This operation is repeated for every location on the input image, resulting in a feature map that highlights the features the kernel was designed to detect. For example, a kernel might be designed to detect horizontal edges in an image, and the resulting feature map would have high values wherever there are horizontal edges in the input image.
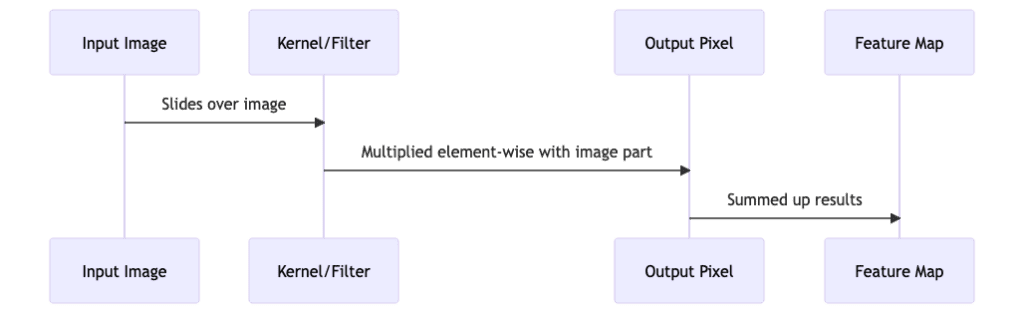
- Input Image slides the Kernel/Filter over itself.
- The Kernel/Filter is then multiplied element-wise with the part of the image it is currently on, resulting in an Output Pixel.
- The results are summed up to give a single output pixel in the Feature Map.
Convolutions in Neural Networks
In a convolutional neural network (CNN), multiple kernels are used to create multiple feature maps from the same input image. Each kernel is designed to detect a different feature, and the collection of all feature maps provides a comprehensive representation of the input image.
Each kernel is designed to detect a different feature, and the collection of all feature maps provides a comprehensive representation of the input image.
This process of convolution and feature extraction is repeated multiple times in a deep CNN, with each layer of the network responsible for detecting more complex features than the last. The first layer might detect simple features like edges and colors, while deeper layers detect more complex features like shapes, textures, or even entire objects.
This hierarchical feature learning is one of the key strengths of CNNs and is a major reason for their success in image recognition tasks. It allows CNNs to automatically learn to recognize complex patterns without being explicitly programmed to do so.
The Role of Convolutions in Overcoming Overfitting
Convolutions also play a crucial role in overcoming overfitting, a common problem in machine learning where a model performs well on its training data but poorly on new, unseen data. Overfitting is often a result of the model learning to recognize noise or irrelevant details in the training data, rather than the underlying patterns.
By extracting and focusing on key features, convolutions help to reduce the dimensionality of the input data, effectively filtering out noise and irrelevant details. This makes the model more robust and improves its ability to generalize to new data.
In our previous articles, we’ve discussed techniques like regularization and dropout that also help in taming overfitting. Convolutions work hand in hand with these techniques to build models that not only perform well on their training data, but also generalize well to new, unseen data.
Breakthroughs Powered by Convolutions
The power of convolutions in neural networks has led to some significant breakthroughs in the field of machine learning. One of the most notable of these is the development of AlexNet, a deep convolutional neural network that won the ImageNet Large Scale Visual Recognition Challenge in 2012.
AlexNet, which we’ve discussed in detail in a previous article, was one of the first models to demonstrate the effectiveness of deep learning for image recognition tasks. It used convolutions to extract features from images and multiple layers to learn complex patterns, setting the stage for the current era of deep learning.
AlexNet was one of the first models to demonstrate the effectiveness of deep learning for image recognition tasks.
Since the development of AlexNet, convolutions have become a standard component of neural networks for image recognition. They’ve been used to build models that can recognize faces, detect objects in real-time video, and even diagnose diseases from medical images.
Challenges and Limitations of Convolutions
While convolutions are a powerful tool in the realm of neural networks, they are not without their challenges and limitations. Understanding these can help us make better use of convolutions and guide us in the search for improvements and alternatives.
Sensitivity to Position and Orientation
One of the main limitations of convolutions is their sensitivity to the position and orientation of features in the input. While this sensitivity allows convolutions to detect local features, it can also lead to problems when the position or orientation of these features changes.
For example, a convolutional neural network trained to recognize a cat might fail to do so if the cat is upside down in the image, even though to a human observer, it’s still clearly a cat. This is because the patterns of pixels that the network has learned to associate with a cat do not match the patterns in the new image. This is normally improved by training convolutions on images that are randomly rotated during training time but this is not always possible, for instance when trying to recognize numbers a six rotated 180 degrees upside down becomes a nine.
Difficulty Handling Different Scales
Convolutions can also struggle to handle features at different scales. A network trained to recognize large objects might fail to recognize the same objects when they are smaller in the image. This is a significant challenge in real-world applications, where the size of objects in images can vary widely.
High Computational Cost
Convolutions, especially in deep neural networks, can be computationally expensive. Each convolution operation involves multiple multiplications and additions, and a network may have millions or even billions of these operations. This can make training and deploying convolutional neural networks resource-intensive, particularly for large datasets and complex models.
Overfitting on Training Data
While convolutions help to reduce overfitting by focusing on key features and reducing the dimensionality of the data, they can still overfit on the training data if not properly regularized. This can lead to poor performance on new, unseen data.
In conclusion, while convolutions are a powerful tool in neural networks, they are not a silver bullet. Understanding their limitations is crucial for effectively using them and for driving the development of new techniques and improvements.
The Mathematics Behind Convolutions
To truly appreciate the power of convolutions, it’s essential to understand the mathematics that underpin them. At their core, convolutions are a simple yet powerful mathematical operation that can extract patterns from complex data.
The Convolution Operation
The convolution operation involves taking a small matrix, known as a kernel or filter, and sliding it over the input data, which in the context of neural networks is typically an image. At each step, the kernel is multiplied element-wise with the part of the image it is currently on, and the results are summed up to give a single output pixel in the feature map.
Mathematically, this can be represented as:
(F * I)(x, y) = ∑∑ F(i, j) * I(x - i, y - j)
where F is the kernel, I is the input image, and the summations are over the dimensions of the kernel. The result is a feature map that highlights the features the kernel was designed to detect.
The Role of the Kernel
The kernel plays a crucial role in the convolution operation. It determines what features are extracted from the input image. For example, a kernel might be designed to detect edges in an image, or more complex patterns like textures or shapes.
The values in the kernel are learned during the training of the neural network, allowing the network to automatically learn to detect the most useful features for the task at hand.
Stride and Padding
Two important concepts in convolutions are stride and padding. The stride is the number of pixels the kernel moves at each step, and it determines how much the kernel overlaps with its previous position. A larger stride results in a smaller feature map and less overlap.
Padding involves adding extra pixels around the input image before performing the convolution operation. This allows the kernel to slide over the edge of the image, resulting in a feature map that is the same size as the input image.
In conclusion, the mathematics behind convolutions is both elegant and powerful, providing a solid foundation for the impressive capabilities of convolutional neural networks.
Convolutions: The Heartbeat of Neural Networks
In conclusion, convolutions are a fundamental part of neural networks, especially those dealing with image data. They transform the raw pixel data of an image into a form that a neural network can understand and process, extracting key features and reducing the dimensionality of the data.
By doing so, convolutions enable neural networks to learn complex patterns, overcome overfitting, and achieve remarkable performance on a wide range of tasks. They truly are the heartbeat of neural networks, pumping information through the network and keeping it alive and learning.
As we continue to explore and understand the intricacies of machine learning, the role of convolutions will undoubtedly remain central. They are not just a tool in the machine learning toolkit, but a powerful force driving the field forward.

Leave a Reply